Úžasné matematické znalosti Archiméda, které ohromují současné odborníky

Život řeckého myslitele byl plný záhad, ale jeho matematické předpovědi stále přitahují pozornost odborníků svou vysokou přesností.
Ztracená kniha mohla změnit historii vědění .
Toto je příběh o ztracené knize, která mohla změnit historii světa. Ztracená před více než dvěma tisíci lety, obsahuje myšlenky jednoho z nejvýznamnějších mozků všech dob. A uplynulo mnoho století, než se jiné mozky dokázaly dostat na stejnou úroveň.
Vše začalo v Syrakusách na Sicílii, v Velké Řecce, v roce 287 př. n. l., kdy se narodil Archimedes, výjimečný génius, pro kterého se zdá, že fráze „předběhl svou dobu“ byla vytvořena speciálně.
„Žádný jiný matematik ve starověku, ani v celé historii, se nemůže srovnávat s Archimédem,“ prohlásil Chris Rores, emeritní profesor matematiky na Drexel University v Pensylvánii, USA, když byl rukopis nalezen.
Snažil se vyřešit problém se zlatou korunou krále. Monarcha měl podezření, že klenotník, který ji vyrobil, do ní přidal levnější stříbro.
Koruna vážila tolik, kolik měla, ale protože stříbro je lehčí než zlato, otázkou bylo, zda byla větší, než kdyby byla vyrobena z čistého zlata.
Říká se, že když Archimedes vstoupil do vany a všiml si, že čím hlouběji se ponořuje, tím více vody z vany vytéká, pochopil, že může určit objem koruny tak, že ji ponoří do nádoby s vodou a změří, kolik tekutiny vytéká.

Říká se, že byl tímto objevem tak nadšený, že okamžitě vyskočil z vany a běžel nahý ulicemi Syrakus, křičíc řecky „Našel jsem to!“.
Termín „eureka“ byl nejznámější ze všech, které tento myslitel vymyslel.
Nevíme, zda obyvatelé Sicílie viděli Archimedovo nahé tělo, ale pravda o královské koruně byla odhalena: klenotník se ukázal jako nepoctivý a Archimedes jako dobrý detektiv.
Během svého života se Archimedes proslavil svými vynálezy a byl známý svými vojenskými zbraněmi.
Král ho jmenoval vojenským poradcem a pověřil ho obranou města. Ale právě v matematice se projevil jeho skutečný genius.
3,14159265358979323846…
Právě on vymyslel hodnotu π, nezbytnou pro výpočet plochy kruhu, jedné ze základních složek vědy.
Udělal to pomocí mnohoúhelníků, protože jejich obvod lze vypočítat, protože jejich strany jsou přímé. Začal tím, že umístil šestiúhelník dovnitř kruhu a další venku. Poté přidával stále více a více stran, až jich bylo 96.
Myšlenka spočívala v tom, že mnohoúhelníky se stále více přibližovaly obvodu kruhu, protože to dávalo pár stále bližších mezí, mezi nimiž se mělo nacházet π.
Výpočet, který zaujal matematiky

Takto vypočítal, že hodnota π se nachází mezi 310 ⁄ 71 (přibližně 3,1408) a 31 ⁄ 7 (přibližně 3,1429), což je odhad, který inženýři používají dodnes a který je pro všechny praktické účely více než dostačující.
Archimedes, posedlý matematikou, neměl příliš ambiciózní úkoly.
Dokonce vypočítal počet zrn písku potřebných k naplnění vesmíru. Odpověď: 10, za kterou následuje 62 nul.
Historici jeho doby vyprávěli, že Archimedes byl nadšený, když objevoval stále složitější matematické formy.
12 čtverců, 8 šestiúhelníků, 6 osmiúhelníků tvoří komolý kubooktaedr…
…12 pětiúhelníků, 30 čtverců a 20 trojúhelníků, 60 vrcholů, 120 hran, 62 stěn: rombosidodekaedr……
a tak dále.
Římská mozaika zobrazuje smrt Archimeda rukou vojáka v Syrakuzách
Archimedova genialita ho proslavila natolik, že se o něm dozvěděli Římané, kteří ho toužili zajmout, aby ho měli ve svých řadách.
Když se jim konečně podařilo vtrhnout do Syrakus, byl vydán rozkaz zajmout Archiméda.
Bohužel, jednomu z vojáků tato zpráva nebyla předána.
Když našel Archiméda, který byl zcela ponořen do svých matematických výpočtů a ani si nevšiml rozruchu kolem sebe, zabil ho svým mečem.
Ničivá transformace
Archimedova smrt v roce 212 př. n. l. znamenala konec zlatého věku řecké matematiky, která postupně upadla.
Archimedova díla však byla zachována díky písařům, kteří kopírovali jeho cenné myšlenky a předávali je z generace na generaci, až byla v 10. století pořízena konečná kopie jeho nejdůležitějších prací.
Zájem o matematiku však byl ztracen. Jméno Archiméda postupně zmizelo.
Jednoho dne v 12. století jednomu mnichovi došel pergamen. Následky byly katastrofální.
Vzal stránky této poslední kopie nejdůležitějšího Archimédova díla, aby je použil k vytvoření modlitební knížky.
Každá stránka rukopisu byla rozřezána, omyta a oškrábána, dokud nebyla dostatečně čistá, aby se na ni dalo psát.
Rukopis byl přepracován a proměnil se v to, co je známé jako palimpsest (z řeckého palin: znovu a psaein: zapisovat).
Výsledek: modlitební kniha kláštera Mar Saba v Judské poušti na Blízkém východě.
Renesance matematiky
Archimedovy učení převzal Leonardo da Vinci
V 15. století přišla do Evropy renesance. Věda pokročila natolik, že vědci byli schopni pochopit Archimedovy matematické argumenty, ale nikdo netušil, že některé z jeho nejbrilantnějších myšlenek byly ztraceny.
Matematici renesance se zabývali koncepty a problémy, které Archimedes vyřešil před 1500 lety.
Uplynulo několik set let, než se o rukopisu znovu začalo mluvit. Nikdo neví jak, ale objevil se v knihovně v Konstantinopoli.
Při prohlížení katalogu knihovny si dánský odborník na řeckou kulturu Johan Ludvig Heiberg všiml jedné věci a v roce 1906 odcestoval do Konstantinopole, aby si prohlédl dokument, který vzbudil jeho zvědavost.
Protože nemohl rukopis z knihovny odnést, Heiberg stránky vyfotografoval a pokusil se Archimedovo dílo rekonstruovat, což bylo neuvěřitelně složité, když měl k dispozici pouze lupu.
Přesto však zjistil, že pod frázemi napsanými středověkými mnichy se zachovaly stopy dosud neznámých myšlenek.
Archimedes nejenže poskytoval odpovědi na své výpočty, ale také zaznamenával své nejskrytější myšlenky a odhaloval, jak svou práci prováděl.
Svou práci nazval „Metoda“.
„Bylo to senzační objev pro historii matematiky. Pokud jste umělec, jistě vás zajímají hotová díla mistrů, ale navíc budete chtít znát techniky, metody a barvy, které používali. Stejně tak matematici chtějí vědět nejen to, jaké byly jejich věty, ale také jak k nim dospěl,“ vysvětlil Rorres.
Žebříky v mysli
Ve svých úvahách formuloval pravdy, jejichž odhalení trvalo mnoho let
„Metoda“ ukázala, že Archimedes vytvořil radikální přístup, který žádný matematik před ním nevymyslel.
Ve své mysli vytvořil sadu zcela imaginárních žebříků pro porovnání objemů zakřivených tvarů. Použil ji, aby se pokusil vypočítat objem koule.
Jelikož objem kužele a válce byl již znám, pokusil se vyvážit kouli a kužel na jedné straně a válec na straně druhé. To vše se odehrávalo v jeho mysli.
Představil si, že provádí nekonečné množství řezů, a pomocí velmi složité matematiky našel způsob, jak vyvážit objekty na stupnici.
Konečný výsledek: objem koule se rovná přesně dvěma třetinám objemu válce, který tuto kouli obklopuje. Tento výsledek považoval za tak důležitý, že požádal, aby byl vyryt na jeho náhrobní desce jako jeho nejdůležitější matematický objev.
Výpočet objemů pomocí nekonečných řezů naznačuje, že Archimedes učinil první krok k důležité oblasti matematiky 1800 let před jejím vynálezem.
Jedná se o matematickou analýzu, bez níž by moderní svět nemohl existovat. Je nezbytná pro vědce a inženýry, na ní závisí technologie 21. století.
Další zmizení
V roce 1914, když byl blízko odhalení skutečného génia Archiméda, vypukla první světová válka. Evropa a Blízký východ se ponořily do chaosu a palimpsest byl opět ztracen.
Vědci téměř nepočítali s tím, že tento dokument ještě někdy uvidí.
V roce 1971 se však britský odborník na klasická studia Nigel Wilson doslechl o stránce rukopisu v knihovně Cambridgeské univerzity a vydal se ji hledat.
„Přepsal jsem několik vět. Obsahovaly velmi specifické technické termíny. Podle slovní zásoby jsem rychle pochopil, že se jednalo o esej Archiméda, a uvědomil si, že to musí být list ze slavného palimpsestu,“ řekl BBC.
Stopy Archimédovy práce lze najít v byzantských větách
Ale proč se v Cambridge objevila pouze jedna stránka Archimédova palimpsestu?
Jednou z nápověd byl její původ: byla součástí sbírky dokumentů, které patřily vědci jménem Konstantin Tishendorf, muži s ne příliš vysokými morálními zásadami.

„Tischendorf hodně cestoval po Blízkém východě. V Konstantinopoli navštívil knihovnu a řekl, že tam zůstala pouze jedna zajímavá rukopis: palimpsest s matematickým textem. Nic víc neřekl,“ poznamenal Wilson.
„Předpokládáme, že tuto stránku ukradl,“ dodal.
Na počátku 20. století měl Heiberg k dispozici pouze lupu, aby mohl rukopis přečíst. V 70. letech měl Nigel Wilson výhodu moderních technologií.
„Většina stránky byla čitelná a pomocí ultrafialové lampy se staly viditelnými rohy, které byly dříve nečitelné.“
Kdyby jen věděli, kde je zbytek rukopisu!
Po první světové válce zaplavily Paříž a další evropská města umělecká díla z Blízkého východu, ale Archimédovo dílo se neobjevilo.
V roce 1991 začal Felix de Marez Oijens, který se později stal známým odborníkem, pracovat v aukční síni Christie’s.
Ve své nové kanceláři našel dopis od francouzské rodiny, která tvrdila, že vlastní palimpsest.
De Marez Oijens byl zvědavý a šel si ho prohlédnout.
Archimedův palimpsest se dostal do Waltersova muzea v Baltimoru
„Okamžitě jsem pochopil, že to musí být rukopis, který Heiberg poprvé studoval v roce 1906,“ řekl BBC.
Majitelé uvedli, že v 20. letech 20. století jejich příbuzný, který byl sběratelem-amatérem, rukopis zakoupil v Konstantinopoli.
Nyní ho chtěli prodat.
Jaká je cena neocenitelného?
„Jakékoli ocenění takového předmětu je pouze odhadem. Myslím, že jsem jim řekl, že má hodnotu od 550 000 do 800 000 dolarů,“ řekl De Marez Oijens.
V roce 1998 za něj anonymní miliardář zaplatil 2 000 000 dolarů.
Díky tomu, že několik měsíců po koupi nový majitel předal rukopis do Waltersova muzea v Baltimoru ve státě Maryland, konečně nastal okamžik, kdy bylo možné obnovit znalosti ztracené před více než dvěma tisíci lety.
Vědci, restaurátoři, klasici a historici se pustili do práce.
Pomocí technologií, jako je multispektrální snímání a rentgenová technika, která způsobuje, že železo ve seškrábaném inkoustu svítí, zjistili, že dokument obsahoval nejen 7 traktátů Archiméda, ale také řeči klasického athénského řečníka Hyperida a komentář k „Kategoriím“ Aristotela z II. nebo III. století n. l.
Mezi traktáty řeckého matematika byla jediná dochovaná kopie Archimedova „Ostomachionu“, ve které se pokouší zjistit, kolika způsoby lze zkombinovat 14 pevných částí, aby vznikl ideální čtverec.
Tento hlavolam má více než 17 000 odpovědí
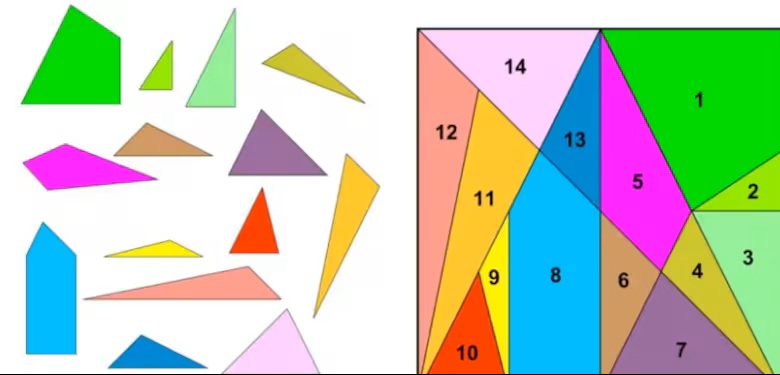
Odpověď je 17 152 kombinací.
Jedná se o první práci na rozvoji matematiky kombinací, která je základem matematiky pravděpodobnosti, která podle všeho vznikla v 17. nebo 18. století.
Do nekonečna
Je pozoruhodné, že čtení „Metody“ jasně ukázalo, že Archimedes učinil velký krok k pochopení nekonečna; navíc použil tento pojem jako součást argumentace v jedné z teorem.
Archimedes byl ještě blíže moderní vědě, než se dříve předpokládalo.
Ačkoli již bylo známo, že učinil některé kroky směrem k moderní matematice, palimpsest ukázal, že v jistém smyslu nejenže ušel velkou část cesty, ale možná již dosáhl cíle.
Co by se stalo, kdyby tento dokument nebyl ztracen? Nebo kdyby se alespoň dostal do rukou matematiků renesance?
„To by samozřejmě změnilo matematiku, ale je třeba vzít v úvahu, že matematika ovlivňuje všechny vědy, takže by to v podstatě bylo jako posunout příliv znalostí o několik set let zpět,“ odpověděl Rores.




